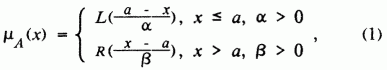
| К оглавлению журнала | |
|
УДК 550.8.01:519.2 |
©И.П. Жабрев, Я.И. Хургин, 1993 |
НЕЧЕТКАЯ
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПРИ ПОДСЧЕТЕ ЗАПАСОВИ.П. ЖАБРЕВ, Я.И. ХУРГИН (ИПНГ РАН)
При построении геологических моделей нефтегазоносных пластов одним из основных источников информации являются данные геофизических исследований скважин (ГИС).
Применяемая сейчас технология обработки данных при ГИС использует стандартную для технических измерений статистическую теорию ошибок измерений. Качество системы обработки данных определяется всей совокупностью вносимых ею ошибок (погрешностей). В теории ошибок измерений принято подразделять совокупную ошибку на несколько компонент (Т.А. Агекян,
1968): случайные, систематические, грубые (промахи) и личные (субъективные).Грубые ошибки
- результат низкой квалификации персонала, небрежности, а также неожиданных сильных внешних воздействий на измерительную систему. Они приводят обычно к очень большим по абсолютной величине погрешностям, которые обнаруживаются и затем исключаются на основе "здравого смысла".Систематические ошибки
- следствие эффектов, действие которых не распознано или не учтено. Они часто оказываются односторонними и характеризуются постоянством или медленным изменением значений. Для их обнаружения и исключения необходимо иметь большие выборки, получаемые в течение длительного времени. Их обнаружение и устранение находятся за рамками статистической теории.Случайные ошибки являются следствием причин, которые невозможно или трудно учесть. В последовательной вероятностно-статистической теории ошибок измерения случайные ошибки считают реализациями случайных величин, т.е. подразумевается наличие распределения вероятностей. Это
- не тривиальное предположение, ибо есть сколько угодно примеров величин, зависящих от случая, но не имеющих распределения вероятностей, например, наличие кворума во время защиты диссертации или измерения в условиях, которые нельзя зафиксировать из-за неконтролируемости переменных внешних воздействий; при этом измерения нельзя многократно проводить в неизменных условиях. Кроме того, предполагается независимость последовательных измерений. Заметим также, что в практике работы при ГИС измерения проводятся однократно. Поэтому оснований для статистической обработки просто нет.Личные ошибки не принадлежат ни к одной из перечисленных компонент. Если в измерениях (оценивании) участвует человек как элемент измерительной системы, то отсутствует возможность неоднократного повторения измерений в неизменных условиях, так как состояние проводящего оценивание человека меняется не только день ото дня, но даже в течение часа. Кроме того, заключения наблюдателя нельзя признать независимыми, ибо они существенно определяются как предыдущей информацией, так и всем жизненным опытом. Поэтому личные ошибки не обладают распределением вероятностей
.Из сказанного следует, что необходимо, прежде всего, обратить внимание на методы обработки данных при ГИС.
Как установлено, при обработке данных ГИС основной вес в общей погрешности измерений среди перечисленных компонент составляют личные ошибки персонала, вносимые как при регистрации, так и при ручной интерпретации [М.Г. Латышева и др.,
1986; 4]. Особое значение имеет работа, проведенная в конце 70-х годов в ЦГЭ; были просчитаны прямые задачи методов электрометрии по различным тестовым ситуациям и затем была решена обратная задача - проведена обработка рядом квалифицированных интерпретаторов. Относительные погрешности при этом оказались для рп до 80 %, для рзп до 60 % и для h до 12%. Этот эксперимент особо интересен, так как здесь нет случайной и систематической составляющих. Таким образом, личные погрешности интерпретации велики. Они оказываются преобладающей компонентой совокупной ошибки интерпретации данных при ГИС. Поэтому использование методов математической статистики при обработке данных ГИС неправомерно. Все сказанное приводит к выводу о необходимости при обработке данных ГИС, а также, очевидно, и полученной другими способами геологической информации отказаться от стандартного применения методов математической статистики и использовать иные подходы.Заметим, что активно внедряемые сейчас компьютерные методы обработки не снимают проблему личных ошибок регистрации и интерпретации данных, а скорее, ее усугубляют, так как они закладывают с самого начала эти личные ошибки в систему обработки, и таким образом любой алгоритм обработки исходно опирается на ненадежную информацию, уточнить которую или уменьшить ошибки за счет подобного алгоритма нельзя.
При подсчете запасов объемным методом следует выделить два этапа:
1) интерпретация данных ГИС с целью получения параметров пласта в каждой исследуемой точке; 2) обработка всего массива параметров, характеризующих пласт, с целью получения адекватных средних величин, моделирующих пласт в целом.Обратим внимание на необходимость обсудить проблему усреднения. Дело в том, что преимущественное использование в геолого-геофизических исследованиях средних арифметических и их модификаций опирается на теорему с том, что стандартное уклонение средней арифметической и независимых случайных величин убывает пропорционально
1/n0.5. Мы считаем, что следует отказаться от применения подобного исходного положения математической статистики.Согласно определению Коши (середина
XIX в), средней нескольких вещественных величин является любая величина, заключающаяся в интервале между самой малой и самой большой из этих величин. К. Джини, один из виднейших статистиков-математиков середины XX в., включает в понятие средней также и процедуру ее получения. В своей книге он приводит около двух десятков аналитически задаваемых средних (средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя экспоненциальная и т.д.) и неаналитических средних (медиана, мода, квартили, децили и т.д.) [I]. Таким образом, сложившаяся ситуация приводит к необходимости изучить вопрос о средних, адекватных геолого-геофизическим задачам, а возможно, и изменить постановки основных задач.Из предыдущего следует, что при подсчете запасов основные параметры пласта нельзя полагать случайными величинами. Поэтому необходимо отказаться от вероятностно-статистической модели ошибок измерения основных параметров пласта. Ее желательно заменить иной моделью, допускающей использование субъективных оценок данных.
Предлагается использовать математический аппарат теории нечетких чисел, развитый в последние
10-15 лет [2, 5].Приведем необходимые определения и факты. Пусть Х
- универсальное множество (элементов любой природы). В классической теории множеств точка х из Х либо принадлежит подмножеству АМX, либо не принадлежит. Однако люди рассуждают не так: месторождения не делятся на большие и малые - вводятся промежуточные градации: очень большие, достаточно малые и т.д. В теории нечетких множеств вводится числовая характеристика mA(х) - степень принадлежности элемента х (например месторождения х) к подмножеству А (например больших месторождений). Функция mA(x) называется функцией принадлежности элемента х к нечеткому подмножеству A. Это описывается в виде упорядоченной пары А = = {х, mA(х)}, х М X.Пусть Х
- это числовая прямая, а - вещественное число. Мы будем рассматривать нечеткое подмножество чисел, примерно равных а: х » а. Такое нечеткое подмножество будем называть нечетким числом.Опираясь на общие положения теории нечетких множеств (см., например,
[3]), можно определить арифметические операции над нечеткими числами. Однако они достаточно громоздки. Д. Дюбуа и А. Прад [2, 5] рассмотрели подкласс, названный ими LR - нечеткими числами.Нечеткое число А называется нечетким числом LR-типа или LR-числом, если его функция принадлежности имеет вид
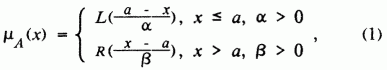
где
L(x) и R(x) - четные, монотонно не возрастающие на положительной полуоси функции: L(0) = R(0) = 1 и обращающиеся в нуль при |х -а| >> 1. Число а характеризует наиболее представительное значение нечеткого числа А - его медиану, моду или его среднее (в одном из многочисленных вариантов понятия средней величины); a и b - левый и правый коэффициенты нечеткости.В дальнейшем для простоты будем рассматривать ситуацию, когда форма левой и правой ветви графика функции принадлежности одинакова
R (х) = L(x), но коэффициенты нечеткости a и b разные, т.е. будем рассматривать LL - нечеткие числа, которые удобно записывать в виде A = (a,a,b).Для практического применения достаточно выбрать какой-либо конкретный класс функций, например,
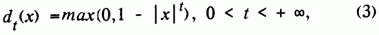
где
t - параметр.Согласно [5], введены арифметические операции над нечеткими
LL - числами.Пусть
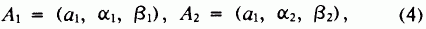
тогда
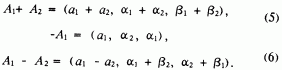
В отличие от операций сложения и вычитания, приводящих вновь к числам LL-типа, произведение АВ и частное А/В, вообще говоря, уже не будут числами
LL-Tuna. Однако, как показано в [5], с точностью малых высшего порядка эти операции вновь приводят к LL-нечетким числам, При этом результаты будут зависеть от знаков сомножителей.Замечание. Интервал (а
- a, а + b), в котором функция принадлежности нечеткого числа положительна, называется носителем нечеткого числа. Дополнительно требуется, чтобы носители сомножителей не содержали нуль.Приведем приближенные формулы для произведения и частного .LL-нечетких чисел, когда их носители расположены на положительной полуоси
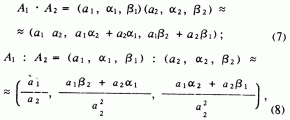
формулы, учитывающие варианты при разных значениях
A1 и А2, см. в [5]. В приложениях естественно коэффициенты нечеткости a и b нечеткого числа А задавать в долях его медианы a = al, b = av, где l, v - обычные числа.Приведем еще одну полезную для дальнейшего формулу, которая получается методом полной индукции из
(7). Пусть задано п нечетких чисел А1,..., Аn, где Аi = (аi, аili, aivi).Обозначим произведение медиан нечетких чисел Аi через
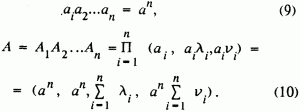
Обсудим теперь применение предлагаемой математической модели в задаче подсчета запасов углеводородного сырья объемным методом. Для определения начальных запасов нефти пользуются формулой
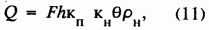
где
F - горизонтальная проекция площади залежи; h - среднее значение вертикальной эффективной нефти (газо) насыщенной толщи пласта; Кп - коэффициент открытой пористости, Кн -коэффициент нефтенасыщенности, q - усадка нефти, рн - плотность нефти.Аналогичная формула применяется и при подсчете объема свободного газа (И.С. Гутман,
1985).Для простоты будем считать величины
q и рн обычными числами, а первые четыре величины в (11) - нечеткими LL - числами, причем для облегчения расчетов будем предполагать их симметричными a = b, тогда (11) примет вид: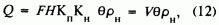 где V = FHKnKн. (13)
где V = FHKnKн. (13)
Пользуясь обозначениями
(2), запишем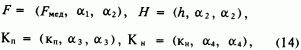
здесь Рмед
- медианное значение нечеткой площади F; H, Кп, Кн - нечеткие числа, характеризующие соответственно толщину пласта и коэффициенты пористости и нефтенасыщенности.Коэффициенты нечеткости
ai даны в (14) в долях медианы соответствующего нечеткого числа: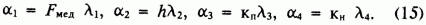
Воспользуемся формулой
(10) для вычисления объема запасов (13), положив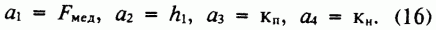
Тогда нечеткое число
V принимает вид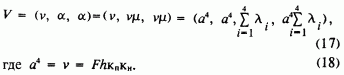
Предположим, что относительные коэффициенты нечеткости
li одинаковы для всех четырех нечетких чисел в (15), тогда при li = l (17) примет вид m = 4l, так чтоV= (v, 4lv, 4lv). (19)
Это означает, что относительные значения коэффициентов нечеткости у нечеткой величины
V, а следовательно, по (12) и у величины запасов Q в четыре раза больше коэффициентов нечеткости, входящих в формулу (12) нечетких чисел, например, если у всех нечетких чисел в (12) (или в (13)) коэффициенты нечеткости l будут равны 0,1, то коэффициенты нечеткости m у запасов будут m = 4l = 0,4, а при значениях нечеткости l = 0,3 коэффициенты нечеткости m у величины запасов Q будут m = 1,2, т.е. при нечеткости каждого из параметров в (12) в 30 % от их медианного значения нечеткость объема будет уже 120 %.В то же время нечеткость каждого из параметров в
(13), определяемых при ГИС, как сказано выше, может достигать и больших величин.Нам представляется, что необходимо пересмотреть традиционные методики подсчета запасов, отказаться от неправомерного использования методов математической статистики и использовать предлагаемый нечеткий подход для оценки возможных ошибок при подсчете запасов
углеводородного сырья и в первую очередь балансовых запасов нефти объемным методом.Нечеткое представление
(12) или (17) дает возможность оценить достоверность получаемой информации и использовать нечеткое представление величины запасов для разработки методов принятия решений более обоснованных, чем традиционные.Следует еще раз подчеркнуть, что предлагаемая нечеткая математическая модель не является усовершенствованием или уточнением традиционной модели, опирающейся на элементарные методы математической статистики.
Авторы считают, что значительный эффект от использования нечеткой математической модели запасов будет получен при анализе ошибок, возникающих при оценке такого сложного параметра, как коэффициент извлечения из недр.
СПИСОК ЛИТЕРАТУРЫ
ABSTRACT
The problem of mathematic statistics methods use during logging data processing is regarded for construction of mathematic model for oil and gas resources calculation. The analysis of common fault components during the models construction is given. The use of not-clear approach for valuation of possible faults during hydrocarbon resources calculation is proposed.