ОЦЕНКА ПОРИСТОСТИ И КОМПОНЕНТНОГО СОСТАВА ПОРОД ПО ДАННЫМ ГИС НА ПЕРСОНАЛЬНЫХ КОМПЬЮТЕРАХ С ИСПОЛЬЗОВАНИЕМ МЕТОДОВ МАТРИЧНОЙ АЛГЕБРЫ

Р.Д. ДЖЕВАНШИР, Т.С. БРЖЕСТОВСКАЯ (ИПГНГМ АН Азербайджана)

Для определения компонентного состава и пористости пород необходимо решить задачу о двух – четырех неизвестных при известных от одного до трех параметров. Наиболее простыми методами для определения литологического состава пород являются двумерные кросс-плоты, учитывающие данные двух геофизических методов. Строящийся в прямоугольных декартовых координатах так называемый z кросс-плот удобен для интерпретации данных о мономинеральных осадочных породах. Когда интерпретируются данные трех методов, на графике кросс-плота необходимо зафиксировать все замеры, т. е. получить трехмерный кросс-плот. Суть его состоит в вычислении величин М и N, зависящих от влияния минерального состава породы на показания различных видов каротажа, отражающих ее пористость [2].

Численное решение задачи о минеральных пропорциях, т. е. о компонентном составе породы и значениях пористости, наиболее эффективно осуществляется как решение систем уравнений, состоящих из соответствующих показаний физических свойств (Dt_1,2,3,d_1,2,3,w_1,2,3) каждого минерала, всей породы (Dt_n, d_n, К_п.n) и их неизвестных пропорций (V₁, V₂, V₃). Решение системы уравнений осуществляется методами матричной алгебры [4, 5]. Ход решения задачи состоит в составлении системы уравнений двух-, трехкомпонентной породы. Для составления алгоритма используются упрощенные формулы определения пористости по каротажам пористостей (АК, ГГК, НК) и формулы для определения полного объема смеси.

Упрощенная формула пористости должна состоять из суммы произведений неизвестных объемов флюидов и составляющих породу компонентов твердой части породы на значения их физических свойств, замеренных соответствующей геофизической аппаратурой, приравненных к показаниям этой аппаратуры в данной смеси. Полный же объем смеси должен состоять из суммы неизвестных объемов, заполненных жидкой (Кп) и твердой (Vтв) фазами породы, приравненных к 1.

Распишем систему для мономинеральной породы. Рассмотрим чистую породу с низкой пористостью, где достаточно применить акустический метод [5]. Известно, что время пробега сейсмической волны, измеренное АК,– линейная функция от пористости. Это отношение обобщенно и выражено уравнением среднего времени:

Кп=Dt–Dt_тв/Dt_ж–Dt_тв, (1) откуда

Dt=КпDt_ж,+(1-Кп)Dt_тв, (2)

где Dt_ж и Dt_тв– соответственно интервальное время пробега упругих волн в жидкости и твердой части породы, мкс/м; Кп – общая пористость породы, доли ед.; (1–Кп) – относительный объем скелетной части породы, т. е. твердой части породы, доли ед.

Для системы уравнений эта формула записывается следующим образом:

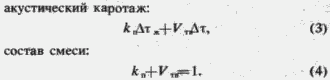
В матричном виде система имеет вид:

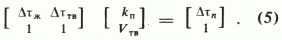
Точность решения системы зависит от констант, входящих в формулу (2) для определения пористости по акустическому каротажу: Dt_ж и Dt_тв. В свою очередь, эти константы определяются экспериментальным путем, где учитывают всевозможные факторы, влияющие на величину замера Dt в жидкости, а также в скелете породы (твердой части или матрице). К этим факторам, в первую очередь, должны относиться минерализация воды, состав самой твердой части породы, минералы, из которых она состоит, глубина залегания породы, от которой зависит влияние геостатического давления, а также тип порового пространства межзерновой, трещинный, каверновый и смешанный. Обычно матричные значения Dt для флюидов и мономинеральных пород берут из литературных источников либо определяются интерпретатором индивидуально для исследуемого района по графикам z кросс-плотов Dt и Кп [1–3].

В чистой породе, но с различным содержанием компонентов, чаще всего доломита и кальцита или доломита и глины, кварца и глины, помимо акустического каротажа можно использовать для определения пористости плотностной ГГК либо нейтронный каротаж. Для учета глинистой компоненты предлагается использовать гамма-каротаж [5]. Все предлагаемые каротажи пористости, а также ГК используются в упрощенном виде по описанному алгоритму. Если применяются АК и ГГК, в этом случае при наличии двух известных, т. е. двух каротажей, мы можем решить задачу с тремя неизвестными: определить количественное соотношение двух компонент породы и ее пористость. Решается система из трех уравнений.

Итак, если применяется плотностной каротаж, то связь объемной плотности горной породы d_n с минеральной плотностью твердой части скелета d_тв и плотностью насыщающей ее жидкости d_ж с пористостью Кп выражается формулой:

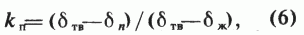
откуда

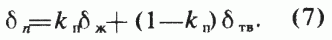
В упрощенной формуле по общему алгоритму эта формула выглядит так:

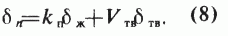
Если твердая часть скелета состоит, например, из минералов кальцита (С) и доломита (Д), то Vтв=Vp+Vд, и тогда формула (8) в расширенном виде для системы уравнений имеет вид:

акустический каротаж:

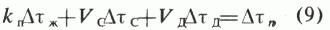
плотностной каротаж:

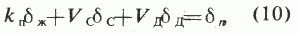
состав смеси:

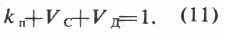
Следует также добавить, что плотностные константы для твердой и жидкой компонент породы также берут либо из литературных источников [2, З], либо получают на основе экспериментальных данных в каждом конкретном случае.

В случае применения нейтронного каротажа связь слабоглинистых полиминеральных карбонатных пород с межзерновой пористостью показаний нейтронного каротажа в общем случае связана с пористостью и минеральным составом следующим уравнением [3]:

где Сизв, Сдол – объемное, содержание соответствующих минералов, доли ед.: (Cизв=Vизв/Vтв, Сдол= Vдол/Vтв); Кп.изв.n, Кп.дол.n характеризуют разницу в значениях истинной пористости известняка, доломита при их одинаковом водородосодержании; Кп.эф – эффективная пористость, доли ед.; (1–Кп) – объем скелетной (твердой части породы), доли ед.; Кп.n– общая пористость, замеренная аппаратурой НК, доли ед.

После упрощения формула (12) имеет вид

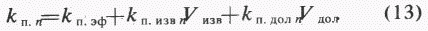
На показания нейтронного каротажа влияет общее водородосодержание w или количество водорода, приходящееся на единицу объема породы, при условии, что водородосодержание пресной воды равно единице. Зная экспериментальные данные, константы по влагосодержанию мономинеральных пород и флюидов [3], формулу (13) можно представить для решения системы уравнений в следующем виде:

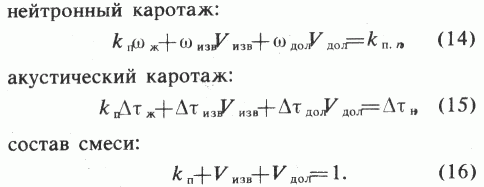
В матричном виде система уравнений выглядит следующим образом:

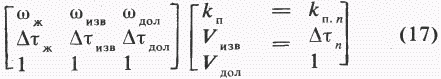
Упрощая формулу (13) до условия, что порода 100 % водонасыщена, водородосодержание жидкой фазы w_ж равно 100 %. Для облегчения решения системы уравнений всегда будем применять это условие. Если учесть, что константы для других минералов, в частности кальцита и доломита, соответственно равны 0 и 4–5 % (для глин 40–50 %, кварца 5 %), то в численном виде формула (13) имеет вид:

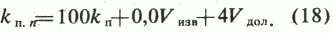
Если порода состоит из трех компонент, то для определения их соотношения используют три вида каротажа. Для численного решения этой задачи необходимо выписать четыре уравнения:

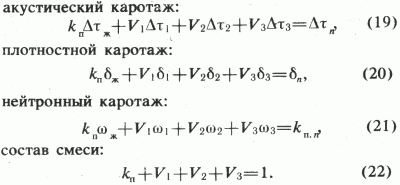
Решение этой системы осуществлено нами на персональных компьютерах с использованием составленных алгоритма и программы [4].

Программа была опробована на месторождениях Тенгиз (скв. 5) и Фахды (скв. 4, Сирия).

Месторождение Тенгиз расположено в восточной части Прикаспийской мегасинеклизы, в интервале залегания среднекаменноугольных пород. Бурение скв. 5 проводилось с использованием промывочной жидкости на нефтяной основе, что ослабило влияние зоны проникновения фильтрата промывочной жидкости на величины геофизических параметров. На основании детального исследования [1] структуры пустотного пространства пород по керну были выделены коллекторы порового, трещинного и каверново-трещинного типов. Присутствие в разрезе коллекторов трещинного и каверново-трещинного типа сказалось на показаниях акустического каротажа хуже, чем на показаниях других методов. Это подтвердилось проведенной корреляцией пористости, определенной по керну, с геофизическими параметрами Dt, dg, и Кп.n. Наиболее надежными методами для оценки общей пористости породы оказался метод НК (коэффициент корреляции r= 0,65), менее надежными – АК и ГГК (r<0,65). Значения пористости по АК были использованы для установления типов коллекторов.

Геологами было установлено, что основными минералами, слагающими разрез подсолевого природного резервуара месторождения Тенгиз, являются кальцит и доломит; чистых глин нет.

Для доказательства предварительного использования кросс-плотов для определения литологического состава разреза были построены графики z кросс-плотов: d и Кп.n; d и Dt; Кп.n и Dt (рис. 1). На графике кросс-плота dn и Dt (см. рис. 1, а) многие пласты с пористостью 3–7 % и низкими значениями Dt (144–164 мкс/м) попали в зону доломитов или вышли за пределы графика. Теоретически это исключено, так как доломиты должны обладать низкой пористостью ( < 3 %). Поэтому предположили, что эта группа пород принадлежит к известнякам или обломочным известнякам, рассеченными трещинами. На графике кросс-плота dn и Dt (см. рис. 1, б) эта же группа замеров (помеченные крестиком) оказалась либо за пределами графика, либо за линией “известняк”, приближаясь к точке “гипс”. Таким образом, картина прояснилась, и было доказано, что породы, помеченные крестиком, не относятся к доломитам, так как обладают плотностью меньшей, чем 2,87 г/см³, а именно 2,4– 2,7 г/см³. Низкие значения Dt подтвердили, что группа пластов относится к известнякам с трещинным типом пустотного пространства. Наилучшее доказательство, что в разрезе среднекаменноугольных пород месторождения Тенгиз преобладают известняки с порово-трещинным и трещинно-каверновым типом коллекторов, дал кросс-плот Кп.n. и dn (см. рис. 1, в).

Таким образом, применив z кросс-плоты, пришли к выводу, что основными минералами, слагающими разрез месторождения Тенгиз, являются кальцит и доломит, что совпало с исследованиями геологов и подтвердило, что, не имея предварительных сведений о минеральном составе пород, построенные вручную кросс-плоты дают достаточно надежные результаты.

По комплексу двух методов пористости (АК+НК или ГГК+НК, или АК+ГГК) можно решить задачу оценки пористости и литологического состава двухкомпонентной породы. Так как в разрезе среднекаменноугольных пород месторождения Тенгиз присутствуют породы с трещинным и каверново-трещинным типом пор, то применение комплекса методов АК+НК для численного решения задачи оценки литологии и пористости оказывается нецелесообразным. Несмотря на это, задачу решили двумя способами, используя комплексы АК+НК и ГГК+НК.

Постоянные коэффициенты для кальцита, доломита и флюида, отражающие плотностные, акустические свойства и водородосодержание брали по литературным данным [1 –3]: соответственно для кальцита 2,71 г/см³, 155 мкс/м, 0,0%; для доломита 2,8 г/см³, 140 мкс/м, 5 %; для флюида 1,1 г/см³, 650 мкс/м, 100 %.

Система уравнений для комплекса методов АК+НК имела вид:

акустический каротаж: 650Кп+155Vс+140Vд=Dt_n. (23)

нейтронный каротаж: 100Кп+0,0Vс+5Vд=Кп.n, (24)

состав смеси: Кn+Vc+Vд=1. (25)

В результате получили практически нулевые значения пористости по всему разрезу и в основном чистые доломиты, в то время как на самом деле разрез представлен обломочными известняками с трещинными типом пустотного пространства.

Для комплекса методов ГГК+НК система уравнений в численном виде записана следующим образом:

нейтронный каротаж: 100Кп+0,0Vс+5Vд=Кп.n, (26)

плотностной каротаж: 1,1Кп+2,71Vс+2,8Vд=dn, (27)

состав смеси: Кп+Vс+Vд=1. (28)

На рис. 2 представлены в графическом виде установленные с помощью ЭВМ литологический состав и пористость разреза скв. 5 месторождения Тенгиз. Полученные по комплексу ГГК+НК результаты совпадают с описанием литологического состава по анализам керна и определенным вручную по графикам z кросс-плотов.

Данные, найденные путем использования наборов различных геофизических методов, подтвердили, что предварительное применение кросс-плотов играет неоценимую роль для выбора оптимального комплекса методов, необходимого для численного решения задачи определения литологического состава и пористости пород.

В качестве другого примера решения задачи оценки литологического состава и пористости пород с помощью системы петрофизических уравнений и методов матричной алгебры были использованы данные по сирийскому месторождению Фахды, представленному свитами нижний Хайян, Рутба, Камшука. Комплекс геофизических исследований скважин представлен акустическим, нейтронным, плотностным и электрическими каротажами.

Для определения литологического состава пород также предварительно построили графики кросс-плотов: Dt и dn, Кп.n и Dt, dn и Кп.n. По ним выяснили, что породы представлены в основном доломитами, реже – известняками и ангидритами, причем известняки с примесью глин. Таким образом, установлено, что порода трехкомпонентна: состоит из минералов кальцита, доломита и глин. Имеющийся набор каротажей пористости (АК, НК, ГГК) и снятые по ним геофизические параметры Dt, kп.n. Dd_g дали возможность определить содержание в породе всех трех компонент, а также ее пористость.

Для определения Dt_гл построили график зависимости Dt и Кп.n, на который нанесли все имеющиеся по данным ручной интерпретации пласты с содержанием глинистого материала 40 % и более, не исключили и плотные пласты. В нашем случае получилось, что Dt_гл=50 мкс/м, которое приняли за Dt скелета глинистой породы. Все остальные константы для глин, доломита и кальцита брались из литературных источников.

В численном представлении система уравнений приняла вид:

нейтронный каротаж: 100Кп+0,0Vc+5Vд+40V_гл=Кп.n., (29)

акустический каротаж: 189Кп+48.8Vc+45.1Vд+50V_гл=Dtn, (30)

плотностной каротаж: 1Кп+2.71Vc+2.86Vд+2.43V_гл=dn, (31)

состав смеси: Кп+Vc+V_д+V_гл=l. (32)

В результате обработки геофизических параметров каждого пласта по имеющейся программе получили графическое представление минерального состава и пористости разреза месторождения Фахды, скв. 4 (рис. 3).

Сопоставления численных результатов машинной интерпретации с данными ручной интерпретации по количественному содержанию минеральных компонентов в породе и результатами пористости, полученными различными методами вручную, показали их идентичность.

В обоих случаях большую разницу составляет время, затраченное на обработку имеющегося материала для решения поставленной задачи вручную и на ЭВМ. Наибольшее преимущество во времени имеет машинная интерпретация, что является основным обоснованием применения матричного подхода для решения задачи определения компонентного состава пород.

СПИСОК ЛИТЕРАТУРЫ

1. Добрынин В.М. Изучение пористости сложных карбонатных коллекторов // Геология нефти и газа.– 1991.– № 5.
2. Интерпретация результатов геофизических исследований нефтяных и газовых скважин. – М.: Недра.– 1988.– С. 426– 441.
3. Кошляк В.А., Семенов Е.В., Жувагин И.Г. Оценка емкостных свойств коллекторов радиоактивными методами.– М.: Недра.– 1988.
4. Определение пористости и компонентного состава пород по данным геофизических исследований скважин (матричный подход) / Л.А. Буряковский, Р.Д. Джеваншир, Т.С. Бржестовская и др. Деп. № 2902-В90.– Баку.– 1990.

ABSTRACT

A matrix approach has been used for accelerated solving the problem of determining the quantitative relation between the components and porosity in the rock. From geophysical well log data, in the Tengiz field (Precaspian megasyneclise) and Fakhdy (Syria) examples, we have obtained, using a computer-aided program, the graphical representations of the mineral composition and porosity of rocks in a sequence of Middle Carboniferous strata and the Lower Khaiyan, Rutba, and Kamshuka formations, respectively. Various combinations of porosity logs have been employed.

РИС. 1. ОПРЕДЕЛЕНИЕ ПОРИСТОСТИ И ЛИТОЛОГИЧЕСКОГО СОСТАВА ПОРОД МЕСТОРОЖДЕНИЯ ТЕНГИЗ (СКВ. 5) ПО ГРАФИКАМ Z КРОСС-ПЛОТОВ: НК-АК (A), ГГК-АК (Б) И ГГК-НК (В).

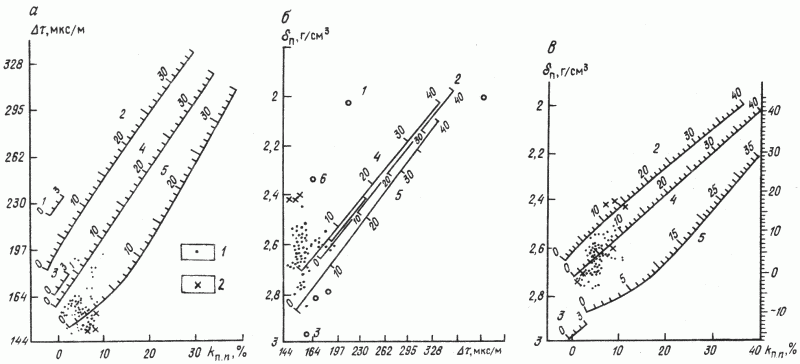
Пласты, охарактеризованные: 1 – по данным ГИС, 2 – по анализам кернов

РИС. 2. МИНЕРАЛЬНЫЙ СОСТАВ И ПОРИСТОСТЬ ПОРОД МЕСТОРОЖДЕНИЯ ТЕНГИЗ (СКВ. 5) ПО ДАННЫМ МЕТОДОВ НК-ГГК:

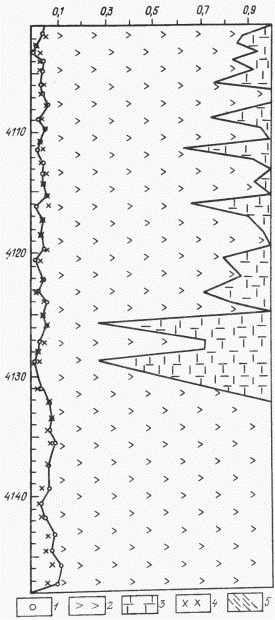
1 – пористость; 2 – кальцит; 3 – доломит; 4 – пористость по керну; 5 – глина

РИС. 3. МИНЕРАЛЬНЫЙ СОСТАВ И ПОРИСТОСТЬ ПОРОД МЕСТОРОЖДЕНИЯ ФАХДЫ (СКВ. 4) ПО ДАННЫМ МЕТОДОВ НК-ГГК-АК.

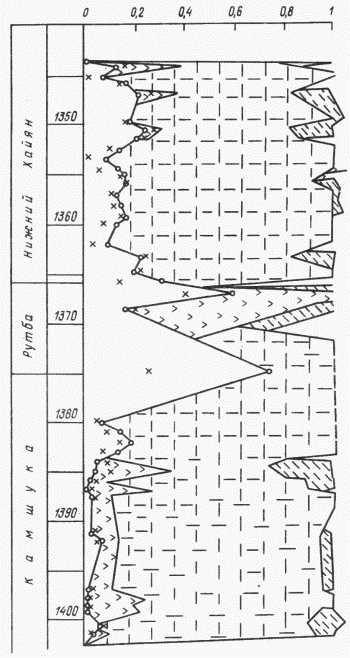
Усл. обозн. см. на рис. 2