Об изучении и классификации коллекторов
В. И. КОЛГАНОВ
Знание физических свойств коллекторов нефти и газа имеет очень большое значение для рациональной разработки нефтяных месторождений, правильного подсчета запасов нефти и газа, изучения процессов нефтеотдачи и т. д.
В данной статье рассмотрены методы исследования структуры порового пространства и поставлена задача на основе двух методик (методики П.П. Авдусина и М.А. Цветковой и метода капиллярной характеристики) вывести объединенную методику изучения и классификации коллекторов.
Для характеристики коллекторов в работе П.П. Авдусина и М.А. Цветковой [1] предлагается изучать эффективную пористость П и гидравлическую характеристику φ породы. Для этого образец породы под вакуумом или давлением насыщают окрашенным бакелитом при температуре, при которой вязкость последнего становится равной вязкости нефти изучаемого месторождения.
Из насыщенного образца изготовляют плоско-параллельный шлиф, на поверхности которого на участке, наиболее типичном в отношении структуры, произвольным радиусом R очерчивают круг S.
В пределах круга определяют суммарную площадь ΣS и суммарную длину периметров Σl сечений пор, заполненных бакелитом.
Отношение суммы площадей сечений пор ΣS ко всей площади выбранного участка шлифа определяет эффективную пористость:

Гидравлической характеристикой структуры порового пространства пород является
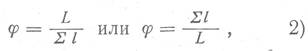
где Σl - суммарный периметр нормальных потоку подвижных веществ сечений поровых пространств, подсчитанный в пределах круга радиуса R; L - периметр сечения цилиндрической (воображаемой) поры, площадь сечения которой равна площади сечения пор в пределах круга радиуса R.
Выражение (2) путем преобразований приводится к удобному для практических исследований виду [5, 6]:

где К - увеличение микроскопа.
Однако формула (3) не совсем точна. Нетрудно убедиться, что если при равномерном распределении пор для подсчета L и Σl брать круги произвольной площади S, то φ будет принимать значения, обратно пропорциональные R. Поэтому все измерения необходимо относить к единице площади шлифа. Для этого случая А.И. Губановым в 1942 г. была выведена и применялась уточненная формула для φ, в которой φ не зависит от площади шлифа S, выбранной для исследования:
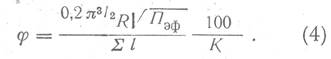
На основе рассмотренной методики авторами предложена классификация коллекторов.
Изучение Пэф и φ проводилось многими исследователями. Нередко Пэф оказывается больше физической (абсолютной) пористости, что говорит о невысокой точности определения ΣS и Σl. Кроме того, сравнение гидравлической характеристики с данными проницаемости показывает, что четкой прямой зависимости между ними нет; установлена лишь общая закономерность: чем больше Пэф и φ, тем больше проницаемость и, наоборот, при малых Пэф и φ проницаемость низкая.
Следовательно, методика не дает точной характеристики фильтрующих свойств песчаников; ее необходимо усовершенствовать.
В последние годы для оценки особенностей строения пористой среды получил распространение метод определения капиллярных давлений при различных насыщенностях образца жидкостью. Сущность метода заключается в том, что насыщенность образца постепенно уменьшают или увеличивают, вследствие чего изменяется кривизна поверхности раздела фаз и, следовательно, капиллярное давление.
Измеряя насыщенность образца и величину капиллярного давления, можно построить кривую зависимости между ними, которая характеризует структуру порового пространства. По капиллярной характеристике можно составить представление об участии пор различного размера в образовании пористости породы, используя известное выражение для капиллярного давления:
![]()
где Рк - капиллярное давление в дн/см2; σ - поверхностное натяжение на границе двух несмешивающихся жидкостей или жидкости и газа в дн/см; θ - краевой угол смачивания; r - радиус поры в см.
Однако в этой методике нет единой величины, по которой можно было бы сравнивать структуры поровых пространств различных пород. Можно сравнивать кривые капиллярных характеристик, но это скорее качественное, чем количественное сравнение.
В обеих методиках поровое пространство изучают с точки зрения оценки размера пор, поэтому вполне естественна и логична попытка объединить их.
Исходным для решения поставленной задачи является выражение
φ= L/ Σl (6)
Для дальнейших преобразований воспользуемся понятием «идеального грунта». Примем, что единицу фильтрующей поверхности в нормальном движении подвижных веществ сечении пронизывает п цилиндрических капилляров радиусом r.
Величины L и Σl выразим через n и r. Периметр отдельной поры, суммарный периметр и суммарная площадь n пор выражаются соответственно:
l=2πr (7)
Σl=n2πr (8)
ΣS=nπr2 (9)
Периметр и площадь воображаемой поры соответственно равны:
L=2πR (10)
S=πR2 (11)
Из определения φ следует равенство площадей ΣS и S, т. е.
nπr2= πR2 (12)
Из равенства (12) следует, что
![]()
Подставляя выражение (13) в формулу (10), получим значение периметра воображаемой поры, выраженное через n и r:
![]()
Подставляя значения Σl и L из формул (14) и (8) в формулу (6), получим
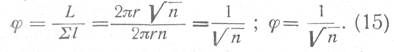
Для дальнейших преобразований решим выражение (5) относительно r:
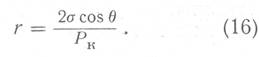
Для „идеального грунта" пористость П через n и r выражается так:
П=nπr2 (17)
Подставляя в формулу (17) значение r и решая полученное выражение относительно n, получим
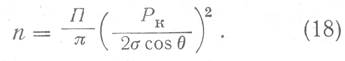
Подставляя значение n в формулу (15), получим окончательное выражение для φ:
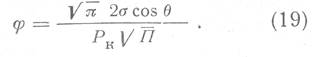
Однако формула (19) получена для однородной структуры порового пространства. Предположим, что на единицу фильтрующей поверхности в нормальном движению подвижных веществ сечении приходится
n1 пор радиуса r1
n2 пор радиуса r2,
n3 пор радиуса r3,
nn пор радиуса rn.
В этом случае, проведя аналогичные преобразования, получим выражение
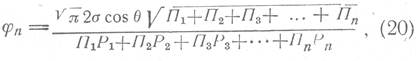
где П1, П2, П3, ... , Пn- пористости, образованные порами радиусов r1,r2, r3,... ,rn, в долях от общего объема породы; P1, Р2, Р3,...,Рn - капиллярные давления для пор радиусов r1,r2, r3,... ,rn
Формулу (20) можно представить в таком виде:
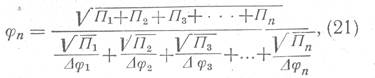
где Δφ1, Δφ1, Δφ1,... Δφn - гидравлические характеристики отдельных элементов структуры порового пространства, определенные по формуле (19) в предположении, что фильтрующую поверхность пересекают как бы только поры одного размера; φn - коэффициент, являющийся гидравлической характеристикой общей структуры, состоящей из совокупности пор различного размера.
Для примера вычислим φn по результатам капиллярного исследования, приведенным в работе К.Г. Оркина [4, стр. 173, табл. 26] (метод - вытеснение воды воздухом).
Объем образца Vобр = 6,15 см3; для воды σ = 72 дн/см; cosθ = 1; 1 мм рт. ст. равен 1333 дн/см.
После подстановки числовых значений формула (20) примет следующий вид:
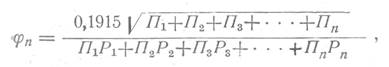
где Рn в мм рт. ст.
Результаты определения φn сведены в таблицу.
Формула (20) объединяет оба указанных метода изучения структуры порового пространства; величина φn (в примере равная 0,00392) является той величиной, которую получил П.П. Авдусин, но определенная на основе капиллярного исследования образца. Для изучения можно брать значительно больший образец породы, что только уточняет фиксацию величины Пn.
Значение величин, входящих в формулу (20), можно определять методом вытеснения воды воздухом [4], но этот метод является длительным (1-2 недели) и, следовательно, неудобным.
Поэтому, как указывает Г.К. Максимович [3], более целесообразно вести опыты не в условиях дренирования воды из керна, а при закачке в образец породы ртути при сравнительно высоких давлениях. Применение для исследований ртути (несмачивающей жидкости) дает характеристику порового пространства с чисто геометрической точки зрения, и, по всей вероятности, можно установить точную связь между коэффициентом φn и проницаемостью породы при фильтрации той же несмачивающей жидкости или воздуха.
Исключение физико-химических явлений при изучении структуры порового пространства лишний раз говорит о преимуществе применения ртутного способа.
Выводы
1. Методика изучения и классификации коллекторов по П.П. Авдусину и М.А. Цветковой в принципе верная, но дает весьма приближенные результаты.
2. Метод капиллярной характеристики более точен, но недоработан математически и не дает единого критерия для классификации коллекторов.
3. Предлагаемая обобщенная методика может служить исходным моментом для классификации коллекторов.
В статье дано только общее теоретическое обоснование методики; детальная разработка ее возможна после проведения большого количества исследований и пересчета имеющихся данных.
4. Наиболее целесообразным лабораторным методом исследования структуры порового пространства является метод закачки ртути в образец с использованием для этого аппаратуры, описанной Г.К. Максимовичем [3]. (При необходимости ее следует дополнить устройством для получения «направленного» насыщения.)
ЛИТЕРАТУРА
1. Авдусин П.П. и Цветкова М.А. О структуре поровых пространств песчаных коллекторов. ДАН СССР, т. 20, № 2-3 1938.
2. Авдусин П.П. и Цветкова М.А. О классификации коллекторов нефти. ДАН СССР, т. 41, № 2, 1943.
3. Максимович Г.К. Теоретические основы процессов вытеснения нефти из пористой среды водой или газом. Нефт. хоз., № 1, 1951.
4. Оркин К.Г. Лабораторные работы по курсу «Физика нефтяного пласта». Гостоптехиздат, 1953.
5. Мирчинк М.Ф. Нефтепромысловая геология. Гостоптехиздат, 1946.
6. Брод И.О. и др. Основы геологии нефти и газа. Гостоптехиздат, 1954.
|
№ п/п |
Капиллярное давление Рn, мм. рт. ст. |
Объем вытесненной из образца воды, см3 |
П1, П2, П3,...Пn |
φ1,φ2,φ3,...φn |
|
1 |
10 |
|
|
|
|
2 |
20 |
- |
- |
- |
|
3 |
30 |
0,050 |
0,00813 |
0,0705 |
|
4 |
40 |
0,025 |
0,00406 |
0,0518 |
|
5 |
50 |
0,075 |
0,01220 |
0,0294 |
|
6 |
60 |
0,100 |
0,01625 |
0,0193 |
|
7 |
70 |
0,200 |
0,03250 |
0,0121 |
|
8 |
80 |
0,300 |
0,04880 |
0,0082 |
|
9 |
100 |
0,175 |
0,0.840 |
0,00675 |
|
10 |
120 |
0,075 |
0,01220 |
0,00318 |
|
11 |
140 |
0,075 |
0,01220 |
0,00568 |
|
12 |
160 |
0,050 |
0,00313 |
0,00527 |
|
13 |
180 |
0,025 |
0,00406 |
0,00510 |
|
14 |
200 |
0,025 |
0,00406 |
0,00490 |
|
15 |
230 |
0,025 |
0,00406 |
0,00470 |
|
16 |
260 |
0,025 |
0,00406 |
0,00448 |
|
17 |
290 |
0,025 |
0,00403 |
0,00425 |
|
18 |
330 |
0,025 |
0,00406 |
0,00405 |
|
19 |
360 |
0,010 |
0,00163 |
0,00392 |
|
20 |
390 |
- |
- |
0,00392 |